Unitary matrix
The case n=2
We call unitary matrices, and denote by $U(2)$ (unitary group) the collection made of them, to those $U\in \mathcal{M}_2(\mathbb{C})$ such that
$$ U\cdot U^{\dagger}=I $$i.e., their conjugate transpose and their inverse coincide. They are the complex counterpart of orthogonal matrices $O(2)$.
Obviously, they satisfy $|det(U)|=1$, since $det(U^{\dagger})=\overline{det(U)}$. And it can be shown (doing simple computations) that they take the form:
$$ U=\left[ \begin{array}{cc}{a} & {b} \\ {-e^{i \varphi} \overline{b}} & {e^{i \varphi} \overline{a}}\end{array}\right], \quad|a|^{2}+|b|^{2}=1 $$Moreover, the linear transformations of $\mathbb{C}^2$ such that they conserve an hermitian inner product defined on it take the form of an unitary matrix when expressed on an orthogonal basis.
If we look at those which specifically verify $det(U)=1$, we get $SU(2)$ (special unitary group), the complex counterpart of rotations $SO(2)$, Any matrix in $SU(2)$ that take the form
$$ U=\left[\begin{array}{cc}{a+i d} & {c+i b} \\ {-c+i b} & {a-i d}\end{array}\right] $$with $a^2+b^2+c^2+d^2=1$, as can be shown by taking any generic matrix and imposing $U\cdot U^{\dagger}=Id$ and $det(U)=1$.
Observe that any such $U$ can be decomposed as
$$ \left[\begin{array}{cc}{a+i d} & {c+i b} \\ {-c+i b} & {a-i d}\end{array}\right]= $$ $$ =a\left[\begin{array}{cc}{1} & {0} \\ {0} & {1}\end{array}\right]+b\left[\begin{array}{cc}{0} & {i} \\ {i} & {0}\end{array}\right]+c\left[\begin{array}{cc}{0} & {1} \\ {-1} & {0}\end{array}\right]+d\left[\begin{array}{cc}{i} & {0} \\ {0} & {-i}\end{array}\right] $$Since the matrices above verify the same product rules as basis quaternions $1, i, j, k$, it turns out that the group $SU(2)$ is isomorphic to unitary quaternions. So, there is a 2 to 1 morphism from $SU(2)$ to $SO(3)$). See relation SO(3) and SU(2).
What is the Lie algebra of $U(2)$?
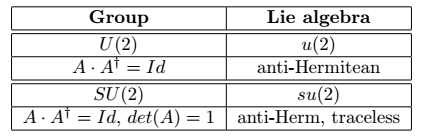
Since $U(2)$ is a group, we can wonder by its Lie algebra, $\mathfrak{u}(2)$.
Considering a curve $A(t)\in U(2)$ with $A(0)=Id$ and differentiating the expression at $t=0$:
$$ A(t)\cdot A(t)^{\dagger}=Id $$we obtain that
$$ A'(0)+A'(0)^{\dagger}=0 $$that is, the elements of $\mathfrak{u}(2)$ are the anti-Hermitian matrices, defined as those which satisfy $B=-B^{\dagger}$. By the way, observe that $B$ is anti-Hermitian if and only if $iB$ is Hermitian matrix.
What is the Lie algebra of $SU(2)$?
Observe that if $A(0)=Id$, then $\left.\frac{d \operatorname{det} A(t)}{d t}\right|_{t=0}=\operatorname{tr} A^{\prime}(0)$ (it can be shown expanding by minors).
Then, if $\det(A(t))=1$,
$$ \operatorname{tr} A^{\prime}(0)=0 $$So the Lie algebra $\mathfrak{su}(2)$ consists of anti-Hermitian traceless matrices.
Any anti-Hermitian matrix can be written as
$$ \left[\begin{array}{cc} {i(a+d)} & {c+i b} \\ {-c+i b} & {i(a-d)} \end{array}\right]= $$ $$ =a\left[\begin{array}{cc} {i} & {0} \\ {0} & {i} \end{array}\right]+b\left[\begin{array}{cc} {0} & {i} \\ {i} & {0} \end{array}\right]+c\left[\begin{array}{cc} {0} & {1} \\ {-1} & {0} \end{array}\right]+d\left[\begin{array}{cc} {i} & {0} \\ {0} & {-i} \end{array}\right]= $$ $$ =a i \mathbf{1}+b \mathbf{i}+c \mathbf{j}+d \mathbf{k} $$and it is traceless if and only if $a=0$, so $su(2)$ corresponds to $\mathbb{R}^3$, and so with $so(3)$, the Lie algebra of SO(3).
These generators
$$ \left[\begin{array}{cc} {0} & {i} \\ {i} & {0} \end{array}\right], \left[\begin{array}{cc} {0} & {1} \\ {-1} & {0} \end{array}\right], \left[\begin{array}{cc} {i} & {0} \\ {0} & {-i} \end{array}\right] $$are called the Pauli matrices, although sometimes they appear multiplied by $-i$.
What is $SU(2)$ topologically?
We have said that $SU(2)$ is isomorphic to quaternions, but we know nothing about it as a manifold or as a topological space. But if we consider the map
$$ U=\left[\begin{array}{cc}{a+i d} & {c+i b} \\ {-c+i b} & {a-i d}\end{array}\right] \longmapsto (a,b,c,d)\in \mathbb{R}^4 $$we have that $SU(2)$ is diffeomorphic to $S^3$ because
$$ det(U)=a^{2}+b^{2}+c^{2}+d^{2}=1 $$So $SU(2)$ is simply connected.
The general case
General facts
The group $U(n)$ consist of complex matrices of rank $n$ ($\mathcal{M}_n(\mathbb{C})$) such that
$$ U\cdot U^*=I $$It can be easily shown that $|det(U)|=1$. But since $det(U)$ is a complex number, the manifold $SU(n)=\{U\in U(n) : det(U)=1\}$ differs in dimension by one with respect to $U(n)$ (unlike the case of orthogonal matrices $O(n)$!!).
The columns of an unitary matrix $U$ form an orthonormal basis of $\mathbb{C}^n$ with the usual Hermitian inner product.
The Lie algebras
Their Lie algebras are denoted, respectively, by $u(n)$ and $su(n)$. Considering $A(t)\in U(n)$ with $A(0)=Id$ and differentiating the expression
$$ A(t)\cdot A(t)^{\dagger}=Id $$we obtain that $$ A'(0)+A'(0)^{\dagger}=0 $$that is, the elements of $\mathfrak{u}(n)$ are the anti-Hermitian matrices, defined as those which satisfy $B=-B^{\dagger}$. By the way, observe that $B$ is anti-Hermitian if and only if $iB$ is Hermitian matrix.
What about $\mathfrak{su}(n)$?
Observe that if $A(0)=Id$, then $\left.\frac{d \operatorname{det} A(t)}{d t}\right|_{t=0}=\operatorname{tr} A^{\prime}(0)$ (it can be shown expanding by minors). Then, if $\det(A(t))=1$,
$$ \operatorname{tr} A^{\prime}(0)=0 $$So the Lie algebra $\mathfrak{su}(n)$ consists of anti-Hermitian traceless matrices.
Generalization
See unitary operator.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: